Attached Code: https://github.com/iainkfraser/PageRank/tree/blogcode
Let's start with a question. How would
you order all websites in order of importance? You could order by
most popular, most informative or most authoritative.
None of those are truly satisfactory
because the question is subjective. It depends on who is asked.
For example I would rank technical, comedy and competitive gaming
sites highly conversely fashion, gossip and liberal arts sites would
rank extremely low. Yet incomprehensible many (majority?) people
think the opposite.
So we alter a websites rank depending
on the viewer. This is what Google does now but originally googled
ranked websites using the PageRank algorithm (named after one of the
founders Larry Page). The algorithm takes an objective approach to
solving the problem.

Figure 1. Random surfer
We have all been there, you go on the
web with a specific purpose and then through a magical Intertubes
journey you end up somewhere totally unpredictable. For example I
started today searching for the relationship between static code
analysis and the halting problem, and I hate to admit ended up on youtube...
Jeez Louise what on earth does that
anecdote have to do with PageRank? Its a nice analogy of how PageRank
works. Given a user (for example a monkey) that surfs the web by
randomly clicking links. The PageRank of a website is the probability
of that user landing on the site after a significant number of
clicks. This is illustrated in Figure 2.
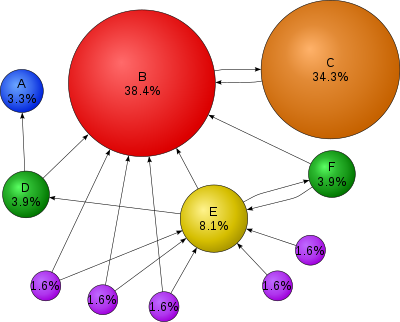
Figure 2. Graph with
PageRank values.
So you can think of
hyper-links as the source website vouching for the destination
website. This explains why website B in Figure 2 is ranked so highly
because many sites link to it. In contrast site C is ranked highly
even though it has only one incoming link. The reason being its got
an incoming link from the big dogg B. Since its likely to land on B it is
also likely to land on C.
“Its not what you know
or who you know – its who knows you.”
Ok that makes sense and if
you're like me you must be wondering how on Gods green earth do you
calculate those probabilities? That is what the rest of the article
is about. First we need Markov chain models. These model the
movement through a stochastic state machines. These are just state
machines with transitions based on probabilities like so:
So just to clarify we can
move from state A to B with probability of 0.5 and from B to C with
1.0 and so on so forth.
The Markov chain is just a
sequence of random variables ( X1, X2, … Xn )
that represent a single state. So you can imagine just walking along
the graph. So let's say we start at state A. Then the random variable
X1 represents our first step so it is
P( X1 = A ) =
0.0
P( X1 = B ) =
0.5
P( X1= C ) =
0.5
The most important feature
of the Markov chain is that the transitions probabilities do not
depend on the past. In this article we assume the transitions are
constant throughout. So it doesn't matter at all what ridiculous
journey you took to get to a state. To predicate the future all you
need is the current state and the transitions. So just to reiterate
the past is irrelevant on Markov chains.
Right let's represent the
state transitions using a transition matrix T . Since the
transitions are probabilities we call it a stochastic matrix (technically the total probability of moving from one state to the
others is 1 so the rows sum to 1).
So the entry at row i and
column j represents the probability of moving from state i to state
j. For example T23 is the probability of
moving from state B to state C i.e. 1.0.
Why did we bother converting
the graph to a matrix. Well it turns out it has a few neat
properties. Let's say we started at state A and I asked you what's the
probability of moving to state C in two steps?
To answer assume the
following notation P(IJ) means the probability of moving from state I
to state J in one step (just look up the matrix). So for example
P(AB) = 0.5. So the probability of going from A to C in two steps is
the probability of going from A to every state (A, B, C) then the
probability of going from that state to C. i.e.
Notice that this corresponds
to the entry T2AC. If you
try it out for the rest of the entries it turns out that the product
of the transition matrix is the probabilities of going from the
row to the column in 2 steps. That is T2ij
the probability of going from state i to state j in two
steps. If you multiply that by the transition matrix you get the
state transitions for 3 steps. So it turns out that Tn
is the state transitions for n steps. Really neat huh? I
thought so anyway.
Ok let's multiply our transition matrix so we can see the probabilities for two, three,
four, five, twenty and one hundred steps:
Something very interesting
happens. The entries seem to converge until all the columns values
become equivalent. This means that after a certain number of steps
it doesn't matter which state you started on. The probability of
getting to another state is constant. My mind = blown. So let's try
visualise this:
Figure 4. State with
converged population distribution.
So let's say we start with a
100 people. Let's use the values of the converged matrix to place people on the graph. So let's put 40% of them on A and another 40% on C. The last
20% can go on B. So move forward one step in the Markov chain.
Half of A will go to B and the other half will go to C. So the new B will have 20% of people. The new C has 20% and the rest of the people from old B which is also 20% therefore the new C has 40%. Finally new state A has all the people from old state C i.e. 40%. Whad'ya know? We are back where we started. So this shows the steady state that the Markov chain converges on. Once we get into this distribution we stay there forever.
Half of A will go to B and the other half will go to C. So the new B will have 20% of people. The new C has 20% and the rest of the people from old B which is also 20% therefore the new C has 40%. Finally new state A has all the people from old state C i.e. 40%. Whad'ya know? We are back where we started. So this shows the steady state that the Markov chain converges on. Once we get into this distribution we stay there forever.
So if the small graph used
in the example actually represented three websites and the related
hyper-links. Then the stabilised values (i.e. the probabilities for
each column in converged matrix) represent the PageRank of each
website. Sweet!
This blog is already long
enough so I'm going to skip over the intuitive proof of convergence.
Although Ive put that in the appendix A. I'll just show how we can use
the transition matrix to calculate the PageRank.
If we represent the initial
distribution (for example of people) using a vector e.g.
That means ¼ of people are
in state A and another ¼ in B and the rest ( ½) are in C. If we
multiply the transition matrix with the vector. We will get a new
vector representing the distribution after the first step. By the
same token if we multiply it by an n step transition matrix then the
result is the distribution after n steps. So written mathematically,
given a transition matrix T, a source distribution s (represented as a row vector) we can calculate the resulting
distribution r after n steps using:
r = s . Tn
So we have two very similar concepts but they are not equivalent.
- After a number of steps the probability of getting to a state is constant regardless of where you start. So no matter what initial distribution you start with you will end up with stable distribution.
- If you apply a single state transition on the stable distribution you will get the stable distribution.
Let's go through both these
points in order. To illustrate point 1 let's pick any random
distribution and multiply it with the stable matrix (the converged
matrix). So let's say we have 0.3, 0.3 and 0.4 in states A,B and C
respectively. Represent it as a row vector and multiply with the
converged matrix:
Notice the result
distribution is the stable distribution. So intuitively what does
this mean? It just means that given the initial distribution and
taking it through a significant number of steps we will eventually
end up at the stable distribution.
The stable distribution is
interesting because once you're in it you remain in that distribution
forever . This just a rewording of point 2. So let's illustrate this
by multiplying the stable distribution with the initial transition
matrix:
Notice we get the stable
distribution again. That makes sense because the definition of the
stable distribution is one that doesn't change when transitioned. If
you try any other distribution on the transition matrix you will not
get the same result.
So if you recall from linear
algebra an eigenvector is a vector that is only scaled when
transformed by a matrix. That is, given a matrix T, a vector s
(called eigenvector)
and a scalar lambda (called eigenvalue) we have
This looks very similar to
our answer above. Except we have a value of lambda as 1 and we are
using a row vector (we could change that by transposing both). So
it turns out that the stable distribution is the eigenvector of the
transition matrix with an eigenvalue of 1.
So moving back to our
PageRank algorithm where the transition matrix is a representation of
the web and the stable distribution is the PageRank of websites. We
can say the PageRank is the eigenvector of the stochastic matrix
representing the topology of hyper-links. Wow! that sounds
complicated but hopefully we now understand what that
means.
Let's generate the algorithm. So our input is the
stochastic transition matrix representing the Web. We want the stable
distribution (i.e. the eigenvector). Remember a multiplication of any distribution with the convergence matrix will be that stable distribution / eigenvector. So all we have to do is multiply any distribution with our convergent matrix to get the answer.
So the problem reduces to finding the convergent matrix. Well we know to do that we just need to multiply repetitively (take to the exponent) the transition matrix until it converges. So let x be our initial distribution. Just set it to 1/n where n is the number of components in the vector (i.e. websites). And we have the following formula to calculate the eigenvector:
Huh? bear with me. Let's expand this out:
So by doing it in this order we can skip a few operations. We can do vector-matrix product instead of matrix-matrix product which has far fewer operations. So the last and final question is when do we stop? when we hit the stable distribution (eigenvector). That is when:
So let's convert this into a floating point friendly algorithm:
/* Inputs are
* n = number of websites
* T = is a n x n transition matrix
*/
vector x = { 1/n, 1/n, ..., 1/n } // initial distribution
do {
old = x
x = x * T
delta = | x - old |
} while( delta > EPISILON );
So once the algorithm is complete, x will be the stable distribution, eigenvector and the PageRank of the web.
So its been a pretty lengthy article for such little code. Always the way with Maths heavy algorithms. For more information on PageRank read "The PageRank Citation Ranking: Bringing Order to the Web" and on Markov chains I highly recommend "Finite Markov Chains and Algorithmic Applications" by Olle Häggström.
So Appendix A has a high-level explanation for convergence. Then Appendix A shows how Google converts the web graph into a Google matrix so that it has a convergent property.
Right I applied the algorithm to the request for comments (RFC) and used citations as links/edges. The PageRank of all RFCs (at the time of writing) in descending order:
https://github.com/iainkfraser/PageRank/blob/master/rfc_pagerank_with_titles.txt
That's all folks - PEACE!
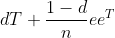
So its been a pretty lengthy article for such little code. Always the way with Maths heavy algorithms. For more information on PageRank read "The PageRank Citation Ranking: Bringing Order to the Web" and on Markov chains I highly recommend "Finite Markov Chains and Algorithmic Applications" by Olle Häggström.
So Appendix A has a high-level explanation for convergence. Then Appendix A shows how Google converts the web graph into a Google matrix so that it has a convergent property.
Right I applied the algorithm to the request for comments (RFC) and used citations as links/edges. The PageRank of all RFCs (at the time of writing) in descending order:
https://github.com/iainkfraser/PageRank/blob/master/rfc_pagerank_with_titles.txt
That's all folks - PEACE!
Appendix A - Convergence
I'm
going to very briefly describe state transition restrictions
that allow convergence. Then i'll explain intuitively why convergence
occurs. If you want to learn more about Markov Chains in more detail then refer to a book, it's a subject in its own right.
Theroem: Any
irreducible and aperiodic Markov chain has exactly one
stationary distribution.
Before I explain irreducible and aperiodic let me say the converse isn't true. Not being irreducible and aperiodic does not mean there isn't a stationary distribution it just means there may not be. So irreducible and aperiodic chains are interesting because we are guaranteed to have stationary distribution (and therefore a PageRank).
Before I explain irreducible and aperiodic let me say the converse isn't true. Not being irreducible and aperiodic does not mean there isn't a stationary distribution it just means there may not be. So irreducible and aperiodic chains are interesting because we are guaranteed to have stationary distribution (and therefore a PageRank).
An
irreducible graph means there is always a way to get from one state
to another eventually. If you can't you call it reducible. Figure 5.
has some example illustrations.
Figure
5. The two chains on the left are reducible and the one on the right
is irreducible
By the
way its called reducible because you can split into two or more
separate graphs and model those using Markov chains. So its quite
obvious there can't be a stationary distribution because remember the
stationary distribution means: the probability of getting from any
state to a certain state is constant. So clearly if you can't get to
a state the probabilities can't be the same because some states can
reach but other(s) cannot.
Figure
6. The two on the right are aperiodic and the left has a period of of
2.
Aperiodic
is a bit more difficult to explain. So I'm going to explain it with
an example, again read one of the Markov chains books for the formal
definition (quickly its the greatest common divisor of the number of
steps to get back to the same state).
So look
at example in Figure 6a. If you place all one hundred people on S1. Then if we do the
next step they all move to S2 (so none on S1). Then they all move back to S1 and so
on and so forth. So clearly its never going to converge because it
oscillates. It has a period of 2, because getting back to state S1
takes a minimum of 2 steps.
Compare
that with Figure 6c which is aperiodic. So S1 is trivial because we can get
straight back to S1 in one step. But S2 we can get back in
2,3,4,5,7... steps. Why isn't that periodic? Let's run through an
instance of a Markov chain. So all 100 people move from S2 to S1.
Then 50 go back S2 and the other 50 stay on S1. Now look at this
distribution (which originally started with 100 on s2) we can get
back to S2 now in 1 step forever. Ergo its not periodic.
So let's
get onto a intuitive description of the proof. If the graph is
aperiodic and irreducible then eventually (after a number of steps)
every value in the transition matrix will be between 0 and 1
exclusively (i.e. not 0 or 1). Because there is a way to get from
any state to any other state.
Figure 7. Probability of moving to B in one step
So let's start thinking of a hypothetical graph shown in Figure 7. I was going to use variables for transition probability but I think numbers are simpler to understand. So if we were playing a game and wanted to get to B in one step we would start at C and if we didn't want to get to B we would start at A. How about two steps?
Figure 8. Probability of moving to B in two steps
So if I asked you to try get to B, what would you say? B->C->B right. Because we already know ending with C -> B is the optimum for one step. So we want the optimum something to C which is B. So the optimum odds of landing on B for 2 steps is 0.54. Notice that the odds are worse than just the single step.
Now if I asked you try to avoid getting to B in two steps what would you say? Well again we want to pick the most likely of landing on A->B (the least likely single step) so we would choose A->A->B which has overall odds of 0.18. Notice again these odds are greater (so in response to the question worst) than the single step.
Figure 9. Probability of A->B in three steps. Notice the minimum is increasing
This illustrates why convergence works. The maximum and minimum probabilities of getting to B will be in the first step. Because in the next step the probability of getting to the maximum step is not 1 so its going to lose a bit (to the other branches). And the probability of getting to the minimum step is also not 1 so we will gain a bit (by the other branches).
Through induction (due to recursive nature of the steps) we can show that after each step the minimum will raise and the maximum will fall until they eventually converge. Therefore no matter where you start you have the same probability of getting to the destination (B in this case).
It should now make sense why you don't want 1 or 0 entries in the matrix forever. Because that means the maximum or minimum doesn't have to fall or raise and thus converge.
Appendix B – Google
Matrix
So we
need the Markov chain to be irreducible and aperiodic to guarantee
that there is a stable distribution (see Appendix 1). An easy way
to do that is to have a link from every state to every other state.
So how
can we transform the hyper-link graph into this type of graph.
Because clearly every website doesn't link every other website. The
way Google does it, is to imagine that the random surfer may get
bored and when that happens they randomly teleport to random website.
So how do
we apply this logic to the transition matrix? Well we need a
probability of the user getting bored call d (for damping) which is
usually set to 0.85 (the clever dudes at Google figured this number
out). Then we can convert the transition matrix to:
So the
dT just dampens all the links due to the chance of getting more bored. Then there is a chance of ( 1 – d ) divided by the number
of sites of randomly teleporting to another site. So we need to add
that to every entry in the matrix which is what eeT (generates a n x n matrix of all ones using outer product).








Great job! If you're interested in a slightly more linear-algebra focused treatment (with proofs), you may want to check out my post on this subject.
ReplyDeletehttp://jeremykun.com/2011/06/18/googles-pagerank-a-first-attempt/
wow! really liked your articles. I recommend interested readers also check them out.
ReplyDeleteWhen I get time ill check out the rest. I'm also interested in improving my Math-programming intersection.
I highly appreciate your hard-working skills as the post you published have some great information which is quite beneficial for me, I hope you will post more like that in the future. 마사지블루
ReplyDeleteThis is really interesting, You’re a very skilled blogger. 건마탑
ReplyDeleteUdaipur Escorts & call girl known for their innocent behavior
ReplyDeleteOur Udaipur Escorts will do precisely what you'll like . Make your day memorable by means of having intercourse with the girls of Udaipur Escorts at some point of lovely surroundings and first-rate surroundings. The girls in our Services are a long way greater, diligent and clearly honest than others.
Udaipur Escorts
Escorts in Udaipur
This website is one thing that is
ReplyDeleteneeded on the internet, someone with a bit of originality!
토토
경마사이트
경마
So nice to find somebody with unique
ReplyDeletethoughts on this subject. Really.. many thanks
for starting this up.
바카라사이트
토토사이트
I find reading this article a joy. It is extremely helpful and interesting and very much looking forward to reading more of your work
ReplyDelete스포츠토토
Hi there, You’ve done an incredible job. I’ll certainly digg it and in my view recommend to my friends. I am confident they’ll be benefited from this site. 경마사이트
ReplyDeleteI could not resist commenting. Well written. There is certainly a lot to learn about this topic. I love all of the points you have made. 야한동영상
ReplyDeleteAlso feel free to visit may webpage check this link
야설
Greetings! Very useful advice within this article! It’s the little changes that will make the biggest changes. Thanks for sharing! 한국야동닷컴
ReplyDeleteAlso feel free to visit may webpage check this link
국산야동
I have to thank you for the efforts you’ve put in penning this blog. I am hoping to check out the same high-grade content from you in the future as well 국산야동
ReplyDeleteAlso feel free to visit may webpage check this link
야설
I have a similar interest this is my page read everything carefully and let me know what you think. 사설토토
ReplyDeleteYour information is helpful for me thanks for sharing the valuable information… 카지노
ReplyDeleteHere you will learn what is important, it gives you a link to an interesting web page: 파워볼
ReplyDeleteI want you that You are a very interesting person. You have a different mindset than the others
ReplyDeleteWant to be rich, then come to see.... พีจีสล็อต สมัคร
"Nice blog here! Also your website loads up very fast! What host are you using? Can I get your affiliate link to your host? I wish my site loaded up as fast as yours lol I frequently read through your articles thoroughly. I’m also interested in wealth generators phone number, you could discuss this occasionally. Have a good day! I’m still learning from you, as I’m trying to reach my goals. I definitely liked reading all that is posted on your blog.Keep the aarticles coming. I liked it!
ReplyDeleteEnjoyed reading through this, very good stuff, thanks." 승인전화없는토토사이트
"It is appropriate time to make some plans for the long run and it’s time to be happy. I’ve read this post and if I may I wish to recommend you some attention-grabbing things or suggestions. Perhaps you could write next articles relating to this article. Thanks for sharing superb informations. Your website is so cool. I am impressed by the details that you’ve on this site.
ReplyDeleteIt reveals how nicely you understand this subject. Bookmarked this web page, will come back for extra articles.
You, I found just the information I already searched everywhere and just could not come across.
What a perfect web site." 검증된놀이터
Woah! I’m really digging the template/theme of this site. It’s simple, yet effective. A lot of times it’s challenging to get that “perfect balance” between usability and appearance. I must say you’ve done a superb job with this. In addition, the blog loads extremely quick for me on Opera. Excellent Blog! This is my very first comment here so I really wanted to say a quick shout out and tell you I truly enjoy reading through your posts. Can you recommend any other sites which go over healthy family diet? I am as well pretty intrigued by this! Thanks a ton! 헤이먹튀
ReplyDeleteThanks for an interesting blog. What else may I get that sort of info written in such a perfect approach? I have an undertaking that I am just now operating on, and I have been on the lookout for such info. You completed a few fine points there. I did a search on the subject and found nearly all persons will go along with with your blog. This is an awesome motivating article.I am practically satisfied with your great work.You put truly extremely supportive data. Keep it up. Continue blogging. Hoping to perusing your next post 우리카지노
ReplyDeleteThank you, I have just been searching for info approximately this topic for a while and yours is the best I have discovered so far. But, what concerning the conclusion? Are you positive in regards to the source? 토토경비대
ReplyDeletePretty good post. I just stumbled upon your blog and wanted to say that I have really enjoyed reading your blog posts. Any way I'll be subscribing to your feed and I hope you post again soon. Big thanks for the useful info. I recently found many useful information in your website especially this blog page. Among the lots of comments on your articles. Thanks for sharing. I've been looking for info on this topic for a while. I'm happy this one is so great. Keep up the excellent work 먹튀폴리스주소
ReplyDeleteGreat post. I was checking continuously this blog and I’m impressed! Very helpful information specially the last part I care for such info a lot. I was looking for this certain information for a very long time. Thank you and good luck.| 엔트리파워사다리
ReplyDeleteThis article is an appealing wealth of useful informative that is interesting and well-written. I commend your hard work on this and thank you for this information. I know it very well that if anyone visits your blog, then he/she will surely revisit it again. Excellent post. I was reviewing this blog continuously, and I am impressed! Extremely helpful information especially this page. Thank you and good luck. this article is very nice and very informative article.I will make sure to be reading your blog more. 토토SOS
ReplyDeleteThis is the type of information I’ve long been trying to find. Thank you for writing this information. 토토사이트
ReplyDeleteThanks on your marvelous posting! I quite enjoyed reading it, you might be a great author. I will ensure that I bookmark your blog and definitely will come back someday. I want to encourage you continue your great job, have a nice afternoon! 카지노
ReplyDeleteThis article is an appealing wealth of useful informative that is interesting and well-written. I commend your hard work on this and thank you for this information. I know it very well that if anyone visits your blog, then he/she will surely revisit it again. I’m impressed, I must say. Actually rarely do you encounter a weblog that’s both educative and entertaining, and let me tell you, you’ve got hit the nail for the head. Your thought is outstanding; the thing is a thing that insufficient consumers are speaking intelligently about. I am happy that I found this at my find some thing with this. Thanks for helping out, good info 카지노사이트
ReplyDeletePretty good post. I just stumbled upon your blog and wanted to say that I have really enjoyed reading your blog posts. Any way I'll be subscribing to your feed and I hope you post again soon. Big thanks for the useful info. I recently found many useful information in your website especially this blog page. Among the lots of comments on your articles. Thanks for sharing. I've been looking for info on this topic for a while. I'm happy this one is so great. Keep up the excellent work 안전토토검증
ReplyDeleteWow that was strange. I just wrote an extremely long comment but after I clicked submit my comment didn’t show up. Grrrr… well I’m not writing all that over again. Anyway, just wanted to say superb blog!| 우리카지노
ReplyDeleteGreat articles and great layout. Your blog post deserves all of the positive feedback it’s been getting. 바카라사이트
ReplyDeleteExtremely pleasant and fascinating post. I was searching for this sort of data and appreciated perusing this one. Continue posting. Much obliged for sharing. When I initially commented I appear to have clicked on the -Notify me when new comments are added- checkbox and now every time a comment is added I get 4 emails with the same comment. Is there an easy method you are able to remove me from that service? Thank you!| 카지노세상
ReplyDeletehi there. Neat submit. There is an hassle along side your internet web page in firefox, and you may need to test this… the browser is the marketplace chief and a massive a part of exclusive people will miss your high-quality writing because of this problem. Super statistics in your weblog, thanks for taking the time to proportion with us. Remarkable perception you've got in this, it's quality to find out a internet site that facts plenty information about special artists. Thanks first-rate article. When i noticed jon’s electronic mail, i recognize the post may be suitable and i'm amazed that you wrote it guy! 토토검증
ReplyDeleteThis an amazing reads, it shows that you actually know what you are talking about, thanks a lot for sharing the elucidate contents.
ReplyDelete온라인카지노
ReplyDeleteI was impressed by your writing. I have a similar hobby as you. 사설토토
I’m very pleased to discover this site. I want to to thank you for ones time for this particularly wonderful read. 파워볼게임
ReplyDelete
ReplyDeleteI like this website its a master peace ! Glad I found this on google . I must say, as a lot as I enjoyed reading what you had to say, I couldn't help but lose interest after a while. Feel free to visit my website;
일본야동
일본야동
국산야동
일본야동
한국야동
ReplyDeleteI must thank you for the efforts you’ve put in writing this blog. I am hoping to view the same high-grade blog posts from you later on as well. In fact, your creative writing abilities has inspired me to get my very own blog now ?? Thank you for the auspicious writeup Feel free to visit my website; 일본야동
일본야동
국산야동
일본야동
한국야동
Your post is very great.i read this post this is a very helpful. i will definitely go ahead and take advantage of this. You absolutely have wonderful stories.Cheers for sharing with us your blog. Feel free to visit my website; 일본야동
ReplyDelete일본야동
국산야동
일본야동
한국야동
Everything is very open with a really clear description of
ReplyDeletethe challenges. It was definitely informative. Your site
is useful. Thanks for sharing! 토토
Hello, just wanted to mention, I liked this article.
ReplyDeleteIt was funny. Keep on posting! 바카라사이트
ReplyDeleteThis website really has all the information I needed concerning this subject and didn’t know who to
ask. 파워볼
I found your blog while I was webs writing to find the above information. Your writing has helped me a lot. I'll write a nice post by quoting your post. Feel free to visit my website; 바카라사이트
ReplyDeleteI want you to thank for your time of this wonderful read!!! I definately enjoy every little bit of it and I have you bookmarked to check out new stuff of your blog a must read blog! Feel free to visit my website; 토토사이트
ReplyDeleteSome really nice and useful information 토토사이트검증 this site, besides I believe the style
ReplyDeleteand design has good features.
Thanks for sharing excellent informations. Your web-site is very cool. I’m impressed by the details that you have on this site. It reveals how nicely you understand this subject. Bookmarked this web page, will come back for more articles. You, my pal, ROCK! I found simply the information I already searched all over the place and simply couldn’t come across. What a great web-site.
ReplyDelete사설토토
토토사이트
Your blog is great. I read a lot of interesting things from it. Thank you very much for sharing. Hope you will update more news in the future.
ReplyDelete토토사이트
토토
You have quoted your thoughts beautifully, and I’m waiting for the upcoming write-up. Till then, create your Personalized Janam kundli by Birth Chart and get astrological assistance.
ReplyDeleteWhy 222 Is a Powerful Sign || free Janam kundli by date of birth
I think this is one of the most significant information for me. And i’m glad reading your article. But should remark on some general things, The web site style is perfect, the articles is really great : D. Good job, cheers 먹튀사이트
ReplyDeletemtgumc
ReplyDeleteI have got you bookmarked to check out new things you post. 파칭코
ReplyDeleteoncasino
ReplyDeleteI do consider all of the ideas you have introduced on your post.
ReplyDeleteThey are very convincing and will certainly work. Visit this WEBSITE and let me know if u enjoy it alot. thank you^^
토토사이트
배트맨토토프로
Thanks on your marvelous posting! I definitely enjoyed reading
ReplyDeleteit, you could be a great author.I will remember to bookmark
your blog and will often come back very soon. I
want to encourage that you continue your great job, have a nice holiday weekend!
스포츠중계
토토
We absolutely love your blog and find nearly all
ReplyDeleteof your post's to be precisely what I'm looking for.
Would you offer guest writers to write content for yourself?
I wouldn't mind publishing a post or elaborating on some of
the subjects you write in relation to here. Again, awesome
weblog!
토토사이트
먹튀검증
온라인카지노
ReplyDelete카지노
I feel like I’ve got useful information from your blog. I feel good. There are lots of useful information on my site. If you have time, please visit once.
Received international standards and is the most high quality website betflix
ReplyDeleteI have read this post and if I could I want to suggest you some interesting things or advice. 카지노사이트
ReplyDeleteAwesome dispatch! I am indeed getting apt to over this info, is truly neighborly my buddy. 카지노사이트
ReplyDeleteHello there! I just wish to offer you a big thumbs up for the excellent info you have got here on this post. 온라인카지노
ReplyDeleteI definitely liked every part of it and i also have you saved as a favorite to see new stuff on your website.호텔카지노
ReplyDeleteI stumble on this site when I was making research on my project topic. I found some useful topics in well detail form. Thanks for this excellent post. 카지노
ReplyDeleteAlong with adjusting the game to be fair to those who come to spin. Make it easy to enter the rewards. give more value So if you want to get to know more slots sites and slots games. You can come and follow the details within this article. pgslot
ReplyDeleteFor the use of G2G8B by playing through the PGSLOT website, although we are a website whose main purpose is to make money. with a variety of games from the website You can bet all year round. By not playing every game from us. Because we have new games update every day, remove the monotony of the same game play, same effects, same soundtracks that you find from other websites if you choose to play. with us
ReplyDeleteบาคาร่า ออนไลน์
If you are someone who has a small amount of money to play. We recommend that you try to obtain free credit slots added to the cost of playing slots Because it will help you to make more money playing games. The more is the type of slot game that can only make money during the free spins. Therefore, you will need to spend quite a lot of money to play. ambbet
ReplyDeleteIn online slots games as well, it is an online gambling game. to rely on techniques to play Whether it's a betting technique, choosing a game, choosing a time to play are all important factors pgslot
ReplyDeleteThe most money-making online gambling game of the era Games that can be played on all platforms ambbet
ReplyDelete
ReplyDeleteบริการเกมสล็อตออนไลน์ปี 2022 เกมให้เลือกเล่นมากกว่า 1,000 เกมสล็อต f สล็อตออนไลน์ ซุปเปอร์สล็อต
The payout ratio is quite good, it is very worthwhile to bet, so we don't want you to miss out on this great gaming camp. pgslot
ReplyDeleteAnd to play games that have all systems of practice to play online games. and both in the android system
ReplyDeleteสล็อตออนไลน์
Then study how to play the basics, it will allow you to learn the different parts already there. Making money wouldn't matter. superslot เครดิตฟรี
ReplyDeletebecause with the method of applying through the automatic system And there is a fast pgslot
ReplyDeletethanks for your nice blog and this good informastion for me. ดูบอลสดฟรี
ReplyDeleteGetting real money or not, it depends on you. select website that can actually make the prize money If you choose a non-standard website สล็อต
ReplyDeleteWe have to buy in spite of the fact that in every online slot game there are free spins. From getting 3 - 5 stacked Scatter symbols pgslot
ReplyDeleteSlot games from the gaming company You can choose to play in a variety. Whether it's an old-themed slot game or a slot game. บาคา
ReplyDeleteHello, admin has something to inform you.
ReplyDeletein a short time We will have a combination of brands.
We will combine all GIANT - GIJ - GLI - together at Giant GAB. สมัครสมาชิกสล็อต pg
Pleasure for players with special features that are unique to each game that allow players to win money back home. joker123
ReplyDelete121Joker123 if you like? Earn money from easy to play gambling games. without having to use your head to plan anything that is very complicated Slots are gambling games. สล็อต
ReplyDelete112 pgslot People who like to play online slots In addition to playing money and winning prizes Playing slots is a good money gamble. บาคา
ReplyDeleteProfessionals love to make money on our website. And our game camp is also very popular. สมัครสมาชิกสล็อต pg
ReplyDeleteackergame, the center of online slots web that is open for all online game services, including slotxo, pgslot, joker123 pgslot เว็บตรง
ReplyDelete
ReplyDelete"I would like to thanks' for the efforts you have put in writing this blog. I’m hoping the same high-grade blog post from you in the upcoming also.
스포츠토토맨은
고스톱사이트
19가이드03
ReplyDeletethis is the best way to share the great article with everyone one, so that everyone can able to utilize this information
스포츠토토맨은
고스톱사이트
19가이드03
ReplyDeleteI was impressed by your writing. Your writing is impressive. I want to write like you
스포츠토토맨은
고스톱사이트
19가이드03
It's very easy to do and can be played with. where you do not need to leave the house sexybacarat
ReplyDeleteby citing various reasons But the problem mentioned above It definitely won't happen to you if you apply for pgslot. สมัครสมาชิกสล็อต pg
ReplyDeleteTo be able to extend the profit from the game Even if there is only a small amount of capital to bet pgslot
ReplyDeleteOnline slots, slots, direct web, slotxo, online games on mobile, deposit - withdraw, top-up with automatic system บาคา
ReplyDeleteFierce adventure and an action-style game that fights for including games in the fantasy genre that will help pgslot เว็บตรง
ReplyDeleteIf you want to be rich, why wait? Apply now! Ready to receive many promotions waiting for you. pgslot
ReplyDeleteHundreds only It is considered a very good website. because there is an easy application process The web system is fast. สมัครสมาชิกสล็อต pg
ReplyDelete777 slot game as it only has a 3-reel format as most experts recommend playing. Bonuses are ข่าวบอล
ReplyDeleteand can also be played through all mobile phones comfortable to play play anywhere Only this can Easy to earn money anytime, anywhere slotxo
ReplyDeletePlaying games that will be able to dare to say that in playing games that buy free spins that are in the matter of what is It is very necessary and in for players slotxo
ReplyDeleteBecause otherwise it may cause the discipline of playing, it is possible. Today, I will introduce Pgslot slots games that can make real money ambbet
ReplyDeletemost popular games that allow players to come and play. And can also confirm OTP, withdraw the most and the latest. because in terms pgslot
ReplyDeleteSlots, shooting fish, arcade games, fishing, gourds, crabs, fish, bingo and dice that are the hottest in 2022. สล็อตxo
ReplyDeletehigh-quality to satisfy you. Your publish changed 파라오카지노쿠폰
ReplyDeleteIt facilitates me very a whole lot to remedy some issues. Thank you for sharing. I like what you men are up too. Such smart work and exposure! Hold up the superb works guys . 사설토토홍보
ReplyDeletei contend with such facts lots. I used to be on 바카라사이트
ReplyDeleteJILI Slot, the most popular new betting website right now Betting game that will make you money overnight. pgslot
ReplyDeleteis a website that chooses slot games to play according to their needs Bored of this game, change that game. You can change without repeating here. jili slot
ReplyDeleteAlthough on the Joker there are online slots that are all good games, but you do not forget that every game would pgslot
ReplyDeleteappreciate it for your hard work. You should keep it up forever! Best of luck. 바카라사이트
ReplyDeletein Thailand. superslot
ReplyDeleteIt also doesn't have to sit and play games indefinitely. to wait for yourself free spins pgslot เว็บตรง
ReplyDeletecountries is exciting You will experience the realism of the train, as if you were actually sitting in a train. ดูบอลสด
ReplyDeleteFirst of all, our employees are strictly 22Mega trained, your problem will be solved. pgslot
ReplyDeleteThere is a theme for 24 hours care and other gambling games that can be played in a full range, such as themes, fruit games, pirate games. pgslot
ReplyDeleteAccess to pg slot mobile, apply now and receive a new signup bonus. Go with old members. ถ่ายทอดสดบอลวันนี้
ReplyDeleteWe carry all the genuine copyright from the mother website directly. not pass agent ผลบอลสด
ReplyDeleteright conditions These free credits will be added to you instantly. but we recommend Ask for details of pgslot
ReplyDeleteHonest, honest to all members. It's a SLOTXO TRUE WALLET website. Pay line. Fast transfer. pgslot เว็บตรง
ReplyDeleteI would like to recommend everyone to hurry and watch the subscription reviews to be part of the JOKER camp. pgslot
ReplyDeleteSlot games break often. The more you can play High payout rates with great promotions Apply today ผลบอลสด
ReplyDeletePay attention to slots, the direct website does not go through our AMBBET agent very much. ดูบอลสด
ReplyDeletePgslot play online slots Play Anytime, Anywhere just have a mobile phone Can be used for both iOS, Android pgslot
ReplyDeleteShoot fish, direct website, not through agents. Play unlimited fun
ReplyDeleteshooting fish straight web pgslot
Just press spin a few times and have a chance to become a millionaire in the blink of an eye. AMBKING
ReplyDeletewho won the club's hip-hop competition. and now famous all over the world It's a video slot game. pgslot
ReplyDeleteWhether it's a direct web slot game, often broken, easily broken, and many others pgslot
ReplyDeleteAuthentic, direct website, Asian slots That has been guaranteed by the casino as a website that is a source of online slots games that meet Asian standards pgslot
ReplyDeletebetting is 10 baht. Return commission on every bill 0.5%, minimum casino 20 Return pgslot
ReplyDeleteThat we still have to rely on external factors.That we still have to rely on external factors. pgslot
ReplyDeleteThank you for sharing useful information with us. please keep sharing like this. “Sambandhah” is made to strengthen your relationship with Counseling Services.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteNice Article. Siddhivinayak Engineering is the most trusted Manufacturer of Shrink Sleeve Applicator Manufacturer
ReplyDeleteThis comment has been removed by the author.
ReplyDeletenice blog. Incepted in the year 2019, We Siddhivinayak Industries are one of the leading Automatic Liquid Filling Machine Manufacturer.
ReplyDeleteand bright aroma in the body that helps therapy, with the research that the smell of roses will help relax and relieve symptoms pgslot
ReplyDeleteBecause it is an online game that can generate extra income in a bang way To players, easy to play, anyone can play. บอลนะจ๊ะ
ReplyDeleteVariety of complete solutions, direct web slots from foreign countries Whether it's a broken game often, a hot game, a game that makes money สล็อตออนไลน์
ReplyDeleteYOUR BLOG* GAVE US A USEFUL INFORMATION TO WORK. YOU HAVE DONE AN AMAZING JOB!
ReplyDeleteI TRULLY APPRECIATE THIS POST. & THIS POST WAS GIVEN TO ME A LOT OF GOOD THOUGHTS. THANKS
ReplyDeleteI LIKE THIS WEBSITE, IT'S ----A MASTERPIECE, IM GLAD THAT I'VE FOUND IT. THANKS...
ReplyDeleteAbogado Conducción Imprudente Condado Monmouth"Your blog post is a breath of fresh air! The positivity and optimism you exude are contagious. Thank you for spreading joy and uplifting others with your wonderful content."
ReplyDeleteNice informative content to read. Thanks for sharing this good post. Divorce Lawyers Loudoun VA
ReplyDeleteImpressive and powerful suggestion by the author of this blog are really helpful to me. Frederick Traffic Lawyer
ReplyDeleteIts a nice analogy of how PageRank works. DUI Attorney Manassas VA
ReplyDeleteYour blogs are really good and interesting. It is very great and informative. Catherine PaneBianco es una artista que explora a través de la fotografía cómo nos conectamos con los demás, con nuestro pasado y con nosotros mismos Bankruptcy lawyers in virginia. I got a lots of useful information in your blog. Keeps sharing more useful blogs..
ReplyDeleteAhmedabad website designing is lending more than 12 years of knowledge for the growth and expansion of your business. We have a full basket of creative branding services like, Website Designing, Website Development, Digital Marketing, SEO Company in Ahmedabad
ReplyDeleteCache Money Hoes appears to be a phrase or combination of words that could be interpreted in different ways depending on the context. It's possible that you're referring to a song lyric, a slang term, or some other specific context.
ReplyDeletevirginia beach personal injury attorney
This comment has been removed by the author.
ReplyDeleteI just read your blog post on Netduma, and I wanted to express my appreciation for the valuable information and insights you've shared.Divorcio Rápido en el Estado de Nueva York
ReplyDeleteWow, I'm genuinely impressed by the quality of content here. It's evident that you put a lot of effort into creating this post. Keep up the excellent work, and thank you for sharing such valuable information. Your dedication to providing valuable content is truly appreciated
ReplyDeleteCómo Presentar Documentos de Divorcio en Nueva York
Because of the first picture only I read the post. Interesting to read and informative too. Keep posting more good informative blogs. Traffic Lawyer in Fairfax VA
ReplyDeleteEl Abogado de Fraude Fiscal es verdaderamente excepcional. Su profundo conocimiento y habilidad legal son impresionantes. Defiende a sus clientes con pasión y eficacia. ¡Altamente recomendado para casos de fraude fiscal en cualquier momento
ReplyDelete
ReplyDeleteI am also very much interested in stationery. I enjoy buying new things. I really like this post. Thanks a lot for posting this post.
Abogado Divorcio Fairfax VA Consulta Gratuita
It depends on who is questioned. For example, I would place a high value on technical, humor, and competitive gaming websites while placing a low value on fashion, gossip, and liberal arts websites. The preceding is a really interesting and timely post. I appreciate the time you spent writing this. You must have done a lot of research and distillation to develop your work. semi truck accident lawyers The information examples and facts are quite useful. I'm convinced that many readers will find this content beneficial.
ReplyDeleteattorney near me
Additionally, stationery piques my curiosity. Purchasing new items is a pastime I enjoy doing. I adore this post so much. Many thanks for sharing this article.Abogados Criminal en el Condado de Prince William
ReplyDeleteThis little step-by-step guide, Thanks for the solution… I was looking for the exact thing ......PPP Loan Fraud Lawyer
ReplyDeleteSecuring Financing for dental offices is crucial for establishing and maintaining a successful practice. Dental professionals often seek loans to cover start-up costs, equipment purchases, and office space. Traditional lenders, such as banks, offer business loans with competitive interest rates, while specialized dental lenders understand the unique needs of the industry. Dentists can also explore government-backed programs or grants aimed at supporting healthcare providers.
ReplyDeleteAdditionally, equipment leasing and practice acquisition loans are popular options. Building a solid business plan, demonstrating financial stability, and maintaining a good credit score enhance the likelihood of approval, ensuring a well-funded and thriving dental practice.
"Surfendipity" is a captivating novel that blends adventure and introspection, creating a captivating story. The well-developed characters add unique flavor to the surf culture backdrop, and the author's descriptive prowess vividly paints the coastal scenes. The themes of self-discovery and passion resonate deeply, making the story relatable on a deeper level. The novel captures the essence of surf culture as a way of life, and despite challenges, it ultimately lands on a shore of inspiration and triumph. "Surfendipity" is a wave of literary brilliance that leaves readers eager for the next wave of the author's storytelling.
ReplyDeleteNueva Jersey Violencia Doméstica
Your blog is a constant source of inspiration with its captivating and insightful content. Your commitment to sharing valuable perspectives is truly impressive. Each post reflects your passion for the subject, turning your blog into a haven of knowledge. Thank you for consistently delivering such enriching and thought-provoking content."Middlesex County Driving Without a License Attorney and Middlesex County Driving Without a License Lawyer
ReplyDeleteNew Jersey divorce law addresses various aspects of marital dissolution,
ReplyDeletedivorce law in new jersey including grounds for divorce, property division, alimony, and child custody. divorce law in new jersey Legal guidance is essential for navigating the complexities of the process.
ReplyDeleteA Fairfax criminal attorney specializes in defending people against a broad range of criminal accusations, so they bring a wealth of experience to the table. Their knowledge covers every area of criminal law, whether you're charged with theft, assault, drug offences, or white-collar crimes. Having a thorough awareness of Virginia's legal system.Fairfax Virginia Criminal Lawyer
Excellent post, we appreciate you sharing this wonderful information with us. Keep it up.criminal attorneys in prince william county
ReplyDeleteIt is my duty as a criminal defense lawyer in Fairfax, Virginia, to make sure that their rights are protected with the utmost dedication and legal knowledge. I'm dedicated to giving them outstanding legal representation in all areas of their criminal case using a client-centered approach.Abogado Defensa Criminal en Fairfax VA
ReplyDelete"Surfing the web becomes an enlightening adventure with 'Surfendipity' on blog.netduma.com. The post delves into the serendipitous discoveries one can make while exploring the vast online realm. The engaging narrative and thoughtful insights showcase the author's passion for the internet's diverse offerings. With a touch of humor, 'Surfendipity' encourages readers to embrace the unexpected and relish the journey of digital exploration. The Netduma blog stands out as a source of inspiration, reminding us all to appreciate the unpredictability that the internet brings into our lives."
ReplyDeleteNew York State Divorce Calculator
commercial contract disputes lawyer
ReplyDelete'Surfendipity' is a captivating book that combines adventure, introspection, and the joy of surfing. The author's narrative is engaging and immersive, drawing readers into the world of surfing and its unexpected connections. The book intertwines personal anecdotes with reflections on the transformative power of nature and the ocean. The author's lyrical prose and vivid descriptions evoke the sights, sounds, and sensations of surfing. However, expanding the narrative to include a broader range of experiences or themes could enrich the storytelling. Exploring the cultural and environmental aspects of surfing destinations would add depth and context to the narrative. Including photographs or illustrations of surf spots and memorable moments would complement the storytelling. The author's passion for surfing shines through in every page, making 'Surfendipity' a must-read for surf enthusiasts and adventurers.
"Surfendipity is more than just a platform; it's a wave of inspiration, a current of creativity, and a community of passionate surfers carving their own paths through the digital sea. With each click, you're carried away on a journey of discovery, where the next perfect wave of content awaits. Here, serendipity meets surf culture, creating an experience that's as exhilarating as catching the perfect wave. Ride the tide of creativity with Surfendipity – where every click is a chance to find something truly extraordinary."
ReplyDeleteNueva Jersey Violencia Domestica Acto
An uncontested divorce in Virginia can cost anywhere from a few hundred to a few thousand dollars, depending on the specific circumstances of the case and the level of legal assistance required. However, it generally remains a more cost-effective option compared to contested divorces, which can involve significantly higher legal fees and prolonged court proceedings. uncontested divorce in Virginia cost
ReplyDeleteThis blog post explores the concept of serendipity, finding good fortune by chance. But moving to Ghaziabad doesn't have to be left to chance!
ReplyDeleteEnsure a smooth transition by letting Grewal Transport Service handle your car shipping. We are Ghaziabad's leading provider of reliable and secure car transport services in Ghaziabad.
Our competitive rates and experienced drivers ensure your car arrives safely and on time, whether you're moving across town or across the country. Focus on exploring the hidden gems of Ghaziabad and let us handle the car logistics. Get a free quote today and experience a stress-free move with Grewal Transport Service!
The blog post discusses the concept of PageRank, a web ranking algorithm that uses the Markov chain model to determine the importance of a webpage based on the likelihood of a random surfer ending up on that page. The algorithm calculates PageRank by iteratively computing the stationary distribution of a Markov chain representing the web graph. It uses a transition matrix (T) to represent the web graph, initial distribution (x), iterative multiplication (T), stopping criteria (epsilon), and interpretation (PageRank). The algorithm ensures a unique stationary distribution and a unique PageRank. dui lawyer clarke va
ReplyDeleteDriving while your license is suspended might be due to a number of factors, such as a complete disdain for the law or a lack of understanding of how serious the offence is. That being said, the risks are still very substantial. The consequences of driving while your license is suspended are harsh and can negatively impact your life for a long time. They include increased fines, prolonged license bans, and even possible jail time.DRIVING ON SUSPENDED LICENSE fairfax
ReplyDeleteSurfendipity is a term that combines the words "surf" and "serendipity," referring to the unexpected joys and discoveries found while surfing or in a beach setting. It can be interpreted in various ways, such as discovering new spots, meeting new friends, and experiencing nature encounters. Surfendipity can also be seen in lifestyle brands, such as beachwear, art, and decor. Events and festivals, such as surf festivals and beach clean-ups, can also be seen as a manifestation of Surfendipity. Travel and tourism can also be seen through surf tours and camps, while media and publications can showcase the beauty of the surf lifestyle. Personal philosophy can also be seen as a reflection of Surfendipity, promoting mindfulness, adventure, and exploration. To incorporate Surfendipity into one's life, one can plan a surf trip, join a surf community, practice mindfulness, and participate in beach clean-ups Robbery Lawyer in fairfax.
ReplyDeleteI'd say 380 ACP like is as good if not better as 9mm for self defence!
ReplyDeleteA local bankruptcy lawyer’s familiarity with the regional court system, judges, and court procedures can be advantageous. They can provide personalized service, ensuring your case is handled efficiently and effectively. By hiring a knowledgeable bankruptcy lawyer nearby, you increase your chances of a favorable outcome, ultimately achieving financial stability and peace of mind. bankrupcty lawyer near me
ReplyDeleteGreat insight. As someone deeply invested in language learning, I completely agree with the points made in this blog.
ReplyDeleteAt Language Gurus, we’ve seen firsthand how access to experienced tutors can transform a student’s language journey. Our platform connects learners with seasoned language experts, offering personalized lessons that cater to individual learning styles and goals. It’s amazing how much progress can be made with the right guidance!
This is such a refreshing take on surfing culture! The idea of embracing the unknown and discovering new spots sounds so exciting.
ReplyDeleteLack of clarity on sex offender registry md exposes residents to potential risks. Without accessible information, safeguarding communities becomes challenging. Utilize the Maryland Sex Offender Registry for instant access to vital data and proactive safety measures. Access the registry now for peace of mind.
"Surfendipity" offers a unique and whimsical experience that blends the thrill of surfing with unexpected moments of joy. The atmosphere is relaxed and welcoming, making it perfect for both seasoned surfers and beginners. Whether it's the serendipitous discovery of a perfect wave or the friendly camaraderie among fellow surfers, "Surfendipity" captures the essence of spontaneous adventure on the water.
ReplyDeleteKing William va traffic lawyer
traffic ticket lawyer King William va
The blog "Surfendipity" offers a captivating blend of surfing culture, adventure, and lifestyle insights. Focused on the world of surfing, the blog provides readers with engaging content ranging from surf spot reviews and tips for improving surfing skills to gear recommendations and ocean conservation topics. New York personal injury lawyer
ReplyDeleteThe trend in educational technology is focusing on personalized and interactive learning experiences, with innovations like AI-driven adaptive learning platforms, immersive AR/VR environments, and blockchain-based credentialing systems. These tools offer personalized content, immersive learning, and global accessibility. However, challenges include equity, data privacy, and teacher training. To fully realize the potential of these technologies, continued research and thoughtful implementation are needed, ensuring equitable access, data security, and effective teacher training.
ReplyDeletevirginia beach family law attorney experienced lawyer with twenty years of experience assisting clients with difficult cases. trustworthy counselor with a strong academic background and expertise in [industry specialties]. devoted to community service, transparent communication, and principled advocacy.
Surfendipity, a term combining the words "surf" and "serendipity," refers to the joyful, unexpected experiences or discoveries experienced while surfing or around the ocean. It could evoke feelings of happiness, peace, ocean adventures, and mindfulness Uncontested Divorce Lawyer New York.
ReplyDeleteSurfendipity is a fantastic blend of creativity and adventure! Their unique approach to surfing brings joy and excitement to every wave, fostering a welcoming community for all skill levels. The positive energy and support among participants create an unforgettable experience, making it a must-try for anyone looking to ride the waves!New Jersey Domestic Violence Registry
ReplyDelete"Surfendipity" is the unexpected joy of discovering new waves, beaches, and surf experiences. Combining "surf" and "serendipity," it captures the thrill of spontaneous adventure in surfing culture. Whether finding hidden surf spots or perfect conditions by chance, it's about embracing the excitement of the unknown in the surfing journey.
ReplyDeleteproperty division attorney fairfax va
If you're a white collar criminal lawyer seeking legal assistance with divorce matters, a divorce lawyer can provide expert advice. Contact us today for more information.
ReplyDeletedinwiddie reckless driving lawyerIn the event that you've been accused of careless driving in Dinwiddie, a talented legal counselor can be your best partner. Careless driving offenses can bring about weighty fines, permit focuses, and even prison time. An accomplished lawyer will completely survey the subtleties of your case, fabricate a strong guard, and supporter for your freedoms in court. They can haggle to possibly diminish punishments or investigate elective goals. Try not to explore what is happening alone — counseling a proficient legal counselor can have a tremendous effect in your result.
ReplyDeleteGreat post! If you find yourself facing a speeding ticket in Arlington, hiring an arlington speeding ticket lawyer can really make a difference. They have the expertise to navigate the local traffic laws and negotiate on your behalf, potentially reducing fines or even getting the ticket dismissed. It’s definitely worth considering to protect your driving record and avoid those hefty insurance hikes. Thanks for sharing such valuable information!
ReplyDeleteFairfax County Bike Accident Lawyer
ReplyDeleteMishaps can be life changing occasions, bringing about actual wounds, profound injury, and monetary strain. Whether it's a fender bender, slip and fall, or working environment injury, exploring the result can overpower. In Fairfax, having an accomplished mishap legal counselor close by can have a huge effect by they way you deal with your case and secure the pay you merit.
Indecent Exposure Maryland Lawyer
ReplyDeleteIn Maryland, obscene openness is characterized as deliberately presenting one's private parts to someone else in a public spot or in a way prone to be seen by others. This offense is commonly named a misdeed, conveying potential punishments including fines and detainment. Factors, for example, the area of the openness and the aim behind it can impact the seriousness of the charge. Guilty parties may likewise confront social shame and long haul results. Legitimate insight is prescribed for those having to deal with such penalties to explore the intricacies of the law.
"Surfendipity" likely combines "surf" and "serendipity," hinting at the unexpected joy and discovery often found while surfing. It could refer to a brand, event, or philosophy that celebrates surfing culture's spontaneous and adventurous spirit. Whether through travel or lifestyle, it emphasizes enjoying the surprises that come with the ocean’s unpredictability.
ReplyDeleteDui Lawyer Prince William County VA
Very Informative! In Maryland, second degree child abuse involves causing physical injury to a child or creating a substantial risk of injury, and it is classified as a serious offense that can lead to significant legal consequences, emphasizing the importance of obtaining experienced legal representation if faced with such charges.
ReplyDeleteNetduma specializes in advanced gaming routers designed to enhance online gaming experiences. With features like geo-filtering and traffic prioritization, it optimizes connectivity for smoother gameplay and reduced latency Traffic Lawyer Rockingham VA This lawyer is highly professional and knowledgeable, providing clear guidance throughout the legal process. Their dedication to clients and strong advocacy make them an invaluable ally in any legal matter
ReplyDeleteLasik Austin Tx, offers individuals a cutting-edge solution for vision correction, utilizing advanced laser technology to reshape the cornea and enhance sight. This procedure has gained popularity due to its potential for rapid recovery and minimal discomfort, allowing patients to quickly resume their daily activities.
ReplyDeleteIn Austin, numerous ophthalmic clinics provide tailored consultations where specialized eye care professionals evaluate each patient’s unique needs and determine their candidacy for the procedure. The city boasts a blend of skilled surgeons and state-of-the-art facilities, ensuring that residents have access to some of the best LASIK options available.
Netduma is an innovative router designed to enhance gaming experiences with advanced features like traffic prioritization and Geo-Filter technology. Its user-friendly interface and powerful performance make it a top choice for gamers seeking a competitive edge southampton traffic lawyer This lawyer is highly professional and knowledgeable, providing clear guidance throughout the legal process. Their dedication to clients and strong advocacy make them an invaluable ally in any legal matter
ReplyDeleteNamah Resort in Ramnagar is a luxury retreat nestled in the lush surroundings of Jim Corbett National Park, Uttarakhand. This 5-star resort offers an ideal escape for nature lovers and adventure enthusiasts. With elegantly designed rooms and suites, guests can enjoy modern amenities and serene views of the surrounding forests and river.
ReplyDeleteThe resort features an outdoor swimming pool, spa services, multi-cuisine restaurants, and an array of outdoor activities, including wildlife safaris, bird watching, and nature trails. Namah Resort Ramnagar is a perfect destination for family vacations, romantic getaways, or corporate retreats, providing a peaceful yet adventurous experience amidst nature's beauty.
I was really happy to find this website!
ReplyDeleteVirginia Criminal Lawyer
virginia criminal defense lawyers
When the legal advisor comprehends the client's requirements, the following stage is fostering a custom fitted lawful technique. This technique depends on current realities of the case, Indian Divorce Lawyers Princeton NJ pertinent regulations, and the reasonable methodology of the contradicting party.
ReplyDeleteThey are prepared to perceive stowed away resources or endeavors at monetary trickiness, for example, Indian Divorce Lawyers Princeton NJ a companion attempting to cover resources or underreport pay. Legal advisors frequently work with measurable bookkeepers if important to reveal stowed away monetary data.
ReplyDeleteWithout a legal advisor, it very well may be challenging to explore the perplexing structures, cutoff times, fathers rights maryland and legitimate language engaged with a separation case.
ReplyDeleteA separation legal counselor has insight in managing these intricacies and can assist with sole custody in maryland arranging a fair settlement or address you in court if essential.
ReplyDeleteA legal counselor can assist you with understanding how this regulation applies to your circumstance, fathers rights marylandwhether you are qualified for spousal help, and what your privileges are in regards to kid care and backing.
ReplyDeleteIf anyone is considering bankruptcy in the Fairfax, VA area, I can’t stress enough how important it is to work with a knowledgeable Bankruptcy Lawyer in Fairfax, VA. I recently went through the process, and having an experienced Bankruptcy Lawyer Fairfax VA by my side made a world of difference. They helped me understand my options, explained the entire process clearly, and worked tirelessly to ensure the best outcome for my financial future. If you’re feeling overwhelmed, consulting with a bankruptcy lawyer is definitely a smart move!
ReplyDeleteIt appears that I couldn’t retrieve more specific information regarding "Surfendipity" from the available sources. Based on a general understanding, Surfendipity could refer to a platform, project, or initiative designed to bring unique and spontaneous surfing content or tools. If you're referring to something specific, such as a website or event, please provide additional details, and I can help refine the description!Dui Lawyer Bland VA
ReplyDeleteThese thoughts demonstrate the team's commitment to enhancing user experiences by providing ideas, guidance, and expert perspectives on networking difficulties. Whether discussing new product features or responding to community feedback, the team's reflections demonstrate their dedication to pushing the boundaries of internet performance.sexual intercourse with minor
ReplyDeleteSurfendipity is more than just a word; it's a celebration of the joyful, spontaneous moments that happen while surfing. It’s about the unexpected thrills of catching the perfect wave, the serendipitous connections made with fellow surfers, and the peaceful harmony found in the rhythm of the ocean. This term encapsulates the magic of those unplanned experiences that make surfing a unique and exhilarating lifestyle. Whether you’re a seasoned surfer or a beginner, Surfendipity embodies the spirit of adventure and discovery that comes with every wave.Chapter 7 or Chapter 13 bankruptcy, these professionals will guide you through each step, ensuring you understand your rights and options. With a focus on providing personalized advice, they aim to protect your assets and help you achieve a fresh financial start. Reach out to skilled Bankruptcy Lawyers in Virginia Beach to take control of your financial future today.
ReplyDeleteGreat article! I love how Surfendipity captures the joy and freedom of surfing while also highlighting the connection to nature. Your tips and stories are so inspiring—makes me want to grab a board and hit the waves! Keep up the awesome work! sex offender registry nyc
ReplyDeleteSurfendipity is a creative blend of "surfing" and "serendipity," capturing the idea of discovering something unexpected and delightful while engaging in surfing or online browsing. It can refer to the happy accidents that occur when exploring the internet, stumbling upon fascinating content or ideas you weren't actively searching for. The term conveys the joy of chance discoveries, whether on the web or while out surfing the waves.
ReplyDeleteDui Attorney Virginia
The lawful counselor will discuss which grounds are fitting for the client's case and brief them on how best to proceed. The partition lawyer moreover surveys whether the client might be equipped for spousal assistance, grounds for emergency custody in md young person support, or care blueprints, and helps them with sorting out their legal opportunities and responsibilities.
ReplyDelete